Integral of e to the 2x

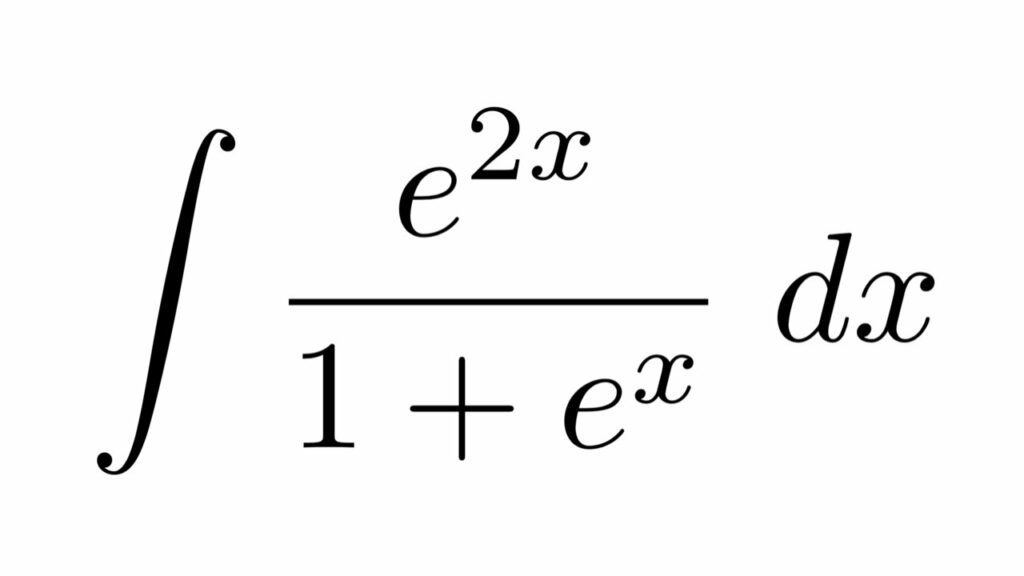
Let’s review some information about e2x before attempting to determine the integral of e to the 2x. It is an exponential function since its exponent contains a variable and its base, “e,” which is a constant (sometimes referred to as Euler’s number). It can alternatively be written as e2x. To get the integral of e to the 2x, we use methods for integrating exponential functions.

Also Read: –What Are The 5 Layers Of Soil

Let’s use various techniques to determine the integral of e to the 2x and use this information to solve a few cases.

The integral of e to the 2x is e^2x/2 + C. This is mathematically written as ∫ e^2x dx = e^2x/2 + C. Here,

• ‘∫’ is the symbol of integration.
• e^2x that is next to dx is the integrand.
• C is the integration constant which is written along with the indefinite integral value of any function.

Common Illusion Regarding Integral of e to the 2x

Do not assume that e2x dx is e2x + C since ex dx = ex + C. The real integral value must always be divided by the x-coefficient. Because x has a coefficient of 2, e2x dx = e2x/2 + C.

Let’s use several techniques to demonstrate that the integral of e to the 2x is e2x/2 + C and then use differentiation to confirm the outcome.

Integral of e to the 2x by Differentiation

We are aware that differentiation and integration operate in the opposite directions from one another. Additionally, we are aware that the integral of a derivative can be calculated using the calculus fundamental theorem. According to this theory, f'(x) dx = f(x) + C. So let’s start by determining the derivative of e2x.

By chain rule,

(e^2x)’ = 2e^2x

Dividing both sides by 2,

(e^2x)’ / 2 = e^2x

By constant multiplication rule of derivatives,

(e^2x / 2)’ = e^2x

Taking integral on both sides,

∫ (e^2x / 2)’ dx = ∫ e^2x dx

Now, by the fundamental theorem of calculus, the integral and derivative symbols get canceled with each other on the left side and we will be left with:

e^2x / 2 + C = ∫ e^2x dx

Hence proved.

Integral of e to the 2x by Substitution Method

The substitution method of integration allows us to get the integral of e to the 2x. Think about the integral e2x dx. In this case, we’ll suppose 2x = u. We obtain 2 dx = du by differentiating on both sides, which is equivalent to writing dx = du/2. The above integral then changes to:

∫ e^u (du/2) = (1/2) ∫ e^u du

We know that the integral of e^x is e^x + C. Using this, the above integral becomes

= (1/2) (e^u + C${}_1$)

= (1/2) e^u + C${}_1$/2

= (1/2) e^2x + C (where C${}_1$/2 = C and u = 2x)

Hence, we have proved that ∫ e^2x dx = (1/2) e^2x + C by using the substitution method.

Since the integrals and derivatives of inverses of each other, to verify the integral of e to the x to be e^2x / 2 + C, we should prove that the derivative of e^2x / 2 + C to be e^2x. Let us find the derivative.

d/dx (e^2x / 2 + C)
= d/dx(e^2x / 2) + d/dx(C)
= (1/2) (2e^2x) + 0 (by the chain rule)
= e^2x

Hence, we have verified the integral of e^2x.

Definite Integral of e to the 2x

An integral with boundaries is a definite integral (lower and upper bounds). The definite integral of e to the 2x from a to b will be taken into consideration. Hence, ab e2x dx. To assess this, we will first take into account the fact that the integral of e2x is equal to e2x/2 + C, following which we will substitute the upper bound and lower bound in turn, one after the other, before subtracting the outcomes. i.e.,

∫ₐ^b e^2x dx = (e^2x/2 + C)ₐ^b

= (e^2b/2 + C) – (e^2a/2 + C)

= e^2b/2 + C – e^2a/2 – C

= e^2b/2 – e^2a/2

= (1/2) (e^2b – e^2a)

Thus, the integration constant doesn’t play any role while calculating the definite integral (because it got canceled).